La compression des images numériques :  le JPEG

Terminale 5S du lycée Camille Claudel de PALAISEAU

Février 2003

Problématique :  Peut-on réduire très fortement la taille des informations décrivant une image numérique, en dégradant de façon contrôlée la qualité visuelle de celle-ci?

Introduction

I - L'image numérique, notions nécessaires à l'exposé

II - Principe mathématique de la compression JPEG

       +Protocole expérimental

III - La perte provoquée de qualité

Conclusion

Introduction

Le JPEG est un format de fichier qui émane des travaux du CCITT (Consultative Committee for International Telegraph and Telephone) et de l'ISO (Organisation Internationnale de Standardisation) formant le groupe de travail JPEG (Joint Photographic Experts Group) et qui aboutit en 1987 au format de fichier qui porte son nom. Il s'agit d'un format libre, c'est à dire qu'il n'appartient à aucune société et est de ce fait gratuit à l'usage. Cela a facilité sa diffusion, il trouve aujourd'hui son application dans divers domaines tels qu'internet, pour lequel il a été conçu. Le JPEG est le premier format à utiliser la méthode de compression dite "avec pertes", s'appuyant sur une dégradation de l'image (concept innovant lors de sa création).
Problématique : Peut-on réduire très fortement la taille des informations décrivant une image numérique en dégradant de façon contrôlée la qualité visuelle de celle-ci?
Nous introduirons dans une première partie les connaissances nécessaires à la compréhension de cet exposé, dans une seconde le principe mathématique de la méthode JPEG et enfin nous nous pencherons sur son aspect plus pratique : la perte provoquée de qualité.

L’image numérique, notions nécessaires à l’exposé  

Notions de base

Une image numérique est constituée de pixels (contraction de l’anglais picture elements), unités d’information de lumière et de couleur qui forment la surface d’une image, très similaire à l’image d’un écran de télévision. Ces couleurs sont codées par un nombre, dont la taille détermine directement le nombre total de couleurs utilisables dans une image : le bit. Par exemple, avec 8 bits, il y a 2*8 possibilités, soit 256 couleurs. Avec si peu de couleurs il est difficile de coder une image complexe telle qu’une photo, ou des dégradés... On admet qu’avec 24 bits, soit 16.777.216 couleurs on possède assez de nuances pour toutes les couleurs visibles par l’œil humain (300.000 couleurs d’après la Compagnie Internationale de l'Éclairage (CIE), l'institut de référence pour l'étude des couleurs qui a commencé ces travaux entre les deux guerres). Une image est aussi définie par sa résolution c'est à dire le nombre de pixels d’une image.

Ainsi avec une image de 640 pixels de largeurs, sur 480 de hauteur, on a : 640x480=307200 pixels. Si  on les code sur 24 bits, on a : 307200 x 24 = 7.372.800 bits soit 921.600 octets (unité informatique, 1 octet = 8 bits). L'image est ici enregistrée au format "BMP" : le format d'image numérique standard, où elle ne subit aucune dégradation ni simplification. Cela signifie que l’on ne peut pas mettre plus d’une image codée ainsi sur une disquette standard (capacité 1.442.304 octets) et que l’on met 4 minutes pour la télécharger avec un modem classique.

Cette image étant de part sa résolution d’une taille (physique) assez réduite, on comprend le besoin de réduire la place occupée par une image numérique pour pouvoir la manipuler sur des supports informatiques (disquettes mais surtout de nos jours Cd-rom, et cartes mémoire d’appareil photo numérique…) mais aussi à travers les réseaux de communication, en particulier Internet. Les  méthodes de compression classiques n'apportant plus un gain de place suffisant,. il nous fallait faire appel à des algorithmes tels que celui utilisé pour le JPEG, dégradant la qualité de l'image avec un facteur contrôlable .

Voici un exemple de résultats attendus :

Qualité 100%, 50% 25% et 1%

Codage RVB vers Luminance chrominance

Le codage a été défini à l’époque où les téléviseurs sont passés à la couleur : par soucis de compatibilité des téléviseurs noirs et  blancs avec les émissions en couleurs on n’a pas transmis les données des 3 couleurs primaires (Rouge Vert Bleu) séparément, mais une image en noir et blanc, avec les données pour la couleur dans un autre signal : Soit un pixel, sa couleur peut-être décomposée avec les 3 couleurs primaires, auxquelles on associe une valeur comprise entre 0 et 255 :

Rouge : E_R  

Vert :  E_V        

Bleu :  E_B

Pour reconstituer la valeur de luminance associée à cette couleur, c'est-à-dire le niveau de gris qui correspond le mieux à la couleur si on la passe en noir et blanc, on utilise la formule suivante :

E_Y=0,30 E_R+0,59 E_V + 0,11 E_B

Lorsque l’on utilise cette valeur de luminance, on a plus qu’à coder deux couleurs, étant donné que la troisième se déduira des deux autres, et de la  valeur de la luminance. Dans la pratique, on soustrait la luminance aux valeurs de ces couleurs, et on les note Dr et Db.

Ainsi :

Db= E_B -E_Y

Dr= E_R - E_Y

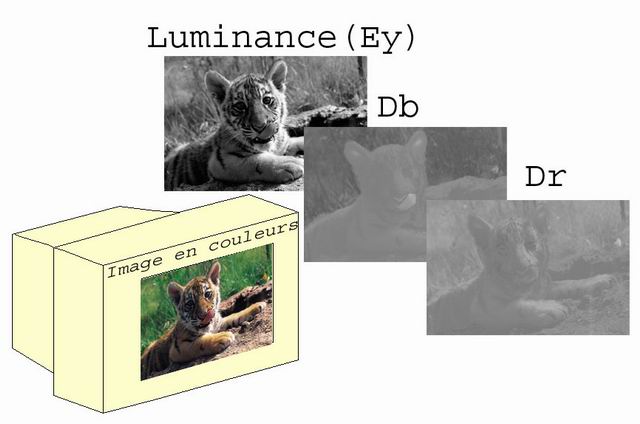
Nous verrons que cette transformation sera exploitée par la suite.    

La compression JPEG

Toutes les étapes sont appliquées à un même exemple :

A) Préparation de l'image

1) Image de départ découpée en blocs de 8x8

L'image de départ est découpée en blocs de 8*8 pixels : c'est à dire en 64 pixels. Au dessus de la valeur de 16*16 pixels, les pixels n'ont plus de relations entre eux ce qui diminue l'efficacité de la méthode de compression JPEG. La valeur de 8*8 a été déterminée, elle apporte de très bons résultats. L'opération  de compression s'effectue donc sur des matrices de 8*8 pixels.

2) Conversion du codage des couleurs en codage Luminance chrominance

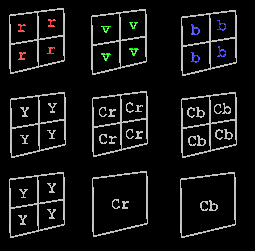
Chaque pixel est codé par 3 composantes : rouge, verte et bleue. C'est le format RVB. Cependant, il n'est à ce stade pas possible de considérer une des composantes comme moins importante par rapport aux autres. On effectue donc une conversion RGB en YUV : Y la luminance de cette couleur, U et V la chrominance de cette couleur dans le rouge et le bleu. Sachant que l'oeil est plus sensible à la luminance qu'à la chrominance. En séparant ces 3 composantes, on pourra dégrader la chrominance tout en conservant la luminance. 3 matrices seront donc obtenues, une de luminance et 2 de chrominance, chacune de 8*8 pixels.

Image 1 : Matrice de luminance de l’image que nous étudierons plus tard.

Image 2 : Matrice des chrominances assemblées.

1                  2

3) Etape de sous échantillonnage

On a vu que l'œil est moins sensible à la chrominance qu'à la luminance. On va donc effectuer une étape appelée sous échantillonnage qui consiste à faire la moyenne dans chacune des 2 matrices de chrominance des valeurs de 4 cases adjacentes, formant un carré. On obtient donc 4 fois moins de valeurs, insérées dans un tableau 4 fois plus petit soit une matrice de 4*4 soit 16 pixels. On réalise ici un gain de place considérable en divisant globalement par 2 la taille de l'image sans perte visible de qualité.

4) Formule DCT

Voici l’étape cruciale de compression JPEG. On applique la transformée en cosinus discrète sur chaque matrice de luminance.

Elle transforme les 64 valeurs spatiales de luminance en 64 coefficients d’amplitude représentant les fréquences spatiales.

Une différence de valeur se caractérise par une période. La fréquence étant l’inverse de la période, à une différence de valeur importante est associée une grande période donc une petite fréquence.

Chaque valeur de cette matrice est le coefficient d’amplitude la caractérisant, c’est en quelques sortes la quantité de motifs identiques que l’on retrouve dans cette portion d’image.

Voici un exemple de bibliothèque de motifs utilisée :  

Prenons l’exemple d’une partie d’image uniforme, c’est à dire représentée par une seule valeur de luminance. C’est un exemple particulier mais réaliste du fait que l’on découpe l’image en blocs de 8*8 pixels limitant ainsi le nombre de motifs différents.

Les petites fréquences sont situées dans la zone inférieure droite de la matrice fréquentielle et les hautes dans la partie supérieure gauche avec la valeur maximale : elle correspond à la composante continue, la constante de l’image. C’est la seule valeur significative. Dans cet exemple, les autres sont nulles.

En quelques sortes, chaque valeur est la quantité de motif dans l’image correspondant à la case où il est situé selon une bibliothèque de motifs comparables. On remarque aussi qu’une majorité des informations codant pour cette image est concentrée dans la zone supérieure gauche car les motifs fins sont rares sur une partie d’image si minime. Cela facilitera considérablement la compression.

5) Quantification

On a vu précédemment que les fréquences les plus faibles correspondant aux motifs fins sont situées dans la partie inférieure droite. L’œil est beaucoup moins sensible à ces derniers qu’aux larges plages uniformes. Ces fréquences vont donc pouvoir être codées avec moins de précision que les autres. On établira une échelle de résolution plus ou moins précise pour les différentes fréquences : c’est la quantification, l’étape où il y a une perte de données. Plus on s’approchera du coin supérieur gauche, plus la précision sera importante. Pour cela, on utilise une table de quantification. Elle va en quelques sortes définir dans quelles proportions cette image sera compressée. En effet pour la créer on utilise la formule suivante : Q(i,j)=1+(i+j+1)*Fq où Fq sera le facteur de qualité. Il variera entre 1 et 10 et plus il sera grand, plus l’image sera compressée au détriment de la qualité visuelle.

Par exemple : Voici la matrice de luminance après la DCT

Voici la table de quantification pour Fq=5

En divisant la matrice par la table de quantification, on obtient ceci, en arrondissant à l’unité près.

Ce qui est à remarquer, est d’une part le nombre de coefficients nuls ainsi que leur position.

6) Le codage.

Cette étape consiste à compresser sans perte de données cette fois ci la matrice obtenue précédemment. Pour cela on utilise le balayage en zigzag suivant :

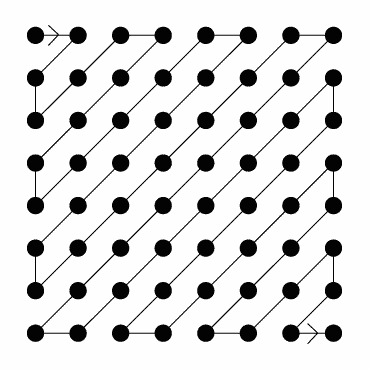
L’algorithme JPEG prévoit ici de compter le nombre de fois qu’une même valeur se répète.

Ce codage appelé « à longueur variable » attribue à une suite de valeur identique une paire de données : la première indique la valeur du coefficient et la deuxième le nombre de fois qu’elle se répète. Ainsi la suite de valeurs 0,0,0,0,0,0,0;2 donne

0, 7;2, 1.

On réalise ensuite une analyse statistique de la suite de chiffres. Elle consiste à attribuer des codes  courts pour des valeurs fréquentes et des codes longs pour des valeurs rares

C’est le codage entropique. Un autre exemple de codage entropique est le morse. Un point est utilisé pour le e courant alors qu’une barre est utilisée pour le q beaucoup plus rare.

Pour mieux comprendre le principe la compression JPEG, voici notre protocole expérimental.

Protocole expérimental d'application de la compression JPEG

1)Numérisation d'un document photographique, et sauvegarde au format « .BMP », afin que l'image ne subisse aucune compression.

2)A l' aide d'un logiciel de dessin, zoomer une partie de l'image et délimiter un bloc de 8x8 pixels.

3)A l'aide du logiciel de dessin, reporter les valeurs pour le rouge, le vert, et le bleu, pour chaque pixel, en utilisant un tableau par couleur. On obtient ainsi trois tableaux de 64 cases, qui représentent les composantes de couleur du bloc de l'image.

4)A l'aide d'un logiciel, on transforme ces composantes en données de « luminance-chrominance »

On obtient 3 tableaux de 64 cases, dont un qui représente la luminance de l'image et les deux autres  qui représentent la chrominance. Pour simplifier, nous ne simplifierons pas la chrominance en tableaux de 4x4, comme le fait le JPEG, et l'on ne détaille que les données de la luminance.

5)On applique la DCT au tableau, et l'on obtient un autre tableau.

6)On divise ces coefficients par la matrice de quantification.

7)Le tableau obtenu contient une grande suite de zéros, qui peuvent être simplifier par un algorithme classique.

8)On applique à ce  dernier tableau obtenu (il y en a en réalité 3) toutes les étapes inverses, et l'on recrée le bloc d'image a partir des données obtenues, que l'on peut ainsi comparer avec le bloc de départ.

Voici l’image de départ.

Le carré noir montre le bloc de 8x8 pixels que l’on va traiter en utilisant un facteur de qualité élevé.

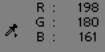
On récupère donc les valeurs de rouge, vert et de bleu pour chaque pixel, et on les rentre dans un tableau :

Matrices RVB : Rouge, Vert, Bleu

Rouge :

Vert :

Bleu :

Matrices Luminance  :

Application de la DCT :

Matrice après quantification :

Matrice après la quantification inverse :

Matrices YUV : Luminance/chrominance

Matrices RVB : Rouge, Vert, Bleu

On ne relève aucune différence notable (aucun écart supérieur à 1). Cela prouve que la méthode de compression JPEG est presque bijective pour un facteur de qualité élevé, avec une image simple (notre bloc ne présente pas d'écarts de couleurs très importants).

Conséquences de la compression JPEG, aspects qualitatifs

Les conséquences de la compression JPEG sont les suivantes :

L'effet "mosaïque"

Comme le JPEG s'applique indépendamment à chaque bloc 8 x 8, il arrive qu'à fort taux de compression les frontières entre les blocs deviennent très visibles.

Qualité 01% (5,74 Ko) Qualité 50% (8,80 Ko) Qualité 100% (28,7 Ko)

Qualité parfaite en bmp : 50 ko.

De plus il arrive que certains blocs soient tellement compressés qu'ils deviennent homogènes. L'image ressemble alors à sa décomposition en blocs, c'est à dire à une mosaïque de carrés de couleur : aussi la qualifie-t-on habituellement de "pixellisée". Elle semble en effet composée de points, comme les images normales, mais il s'agit ici de macro points, qui sont les blocs en réalité.

Les différences de couleur indécelables

De faibles variations de couleur sont indécelables à l’œil humain.

Voici deux carrés de couleur :

Ces 2 carrés ont l’air identiques à première vue.

Il s’avère que l’un est du noir pur c’est à dire codé en RGB par (0-0-0) et l’autre du noir codé par (10-10-10).

L'incapacité qu'a notre oeil à déceler cette différence de couleur est révélatrice des possibilités de simplification du JPEG.

Conclusion

En conclusion, le JPEG utilise une multitude de méthodes astucieuses et un algorithme mathématique, afin de sélectionner avec pertinence les zones de l'image les plus significatives, et ainsi de rendre quasi-invisibles les imperfections visuelles dues aux informations simplifiées ; cela fait que cette méthode de compression d'images numériques est la plus utilisée actuellement.

Références :

-Les secrets de l’image vidéo, par Philippe Bellaïche, aux éditions Eyrolles.

-http://www.jpeg.org/public/jpeglinks.html

-http://iphilgood.chez.tiscali.fr/Codage/Compressionjpeg.htm

-http://www.chez.com/nico77/DossierJPEG.htm (attention, inexactitudes)

-http://membres.lycos.fr/compressionimg/JPEG.htm

-http://www.iee.et.tu-dresden.de/iee/hpsn/lv/procdesign/jpeg/sim/source.html

-http://xavier.chassagneux.free.fr/tipe/tipe.htm

-http://www.chez.com/algorithmejpeg/gene.htm